In mathematics, differential rings, differential fields and differential algebras are rings, fields and algebras equipped with a derivation, which is a unary function satisfying the Leibniz product law. A natural example of a differential field is the field of rational functions over the complex numbers in one variable, C(t), where the derivation is differentiation with respect to t.
Differential ring
A differential field is a field K, together with a derivation. The theory of differential fields, DF, is given by the usual field axioms along with two extra axioms involving the derivation. As above, the derivation must obey the product rule, or Leibniz rule over the elements of the field, in order to be worthy of being called a derivation. That is, for any two elements u, v of the field, one has

since multiplication on the field is commutative. The derivation must also be distributive over addition in the field:

If K is a differential field then the field of constants


 Differential field
Differential fieldA differential algebra over a field K is a K-algebra A wherein the derivation(s) commutes with the field. That is, for all
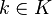 and
and 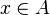 one has
one has
In index-free notation, if
 is the ring morphism defining scalar multiplication on the algebra, one has
is the ring morphism defining scalar multiplication on the algebra, one has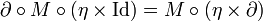
As above, the derivation must obey the Leibniz rule over the algebra multiplication, and must be linear over addition. Thus, for all
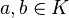 and
and  one has
one has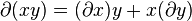
and
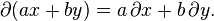
Differential algebra
If A is unital, then ∂(1) = 0 since ∂(1) = ∂(1 × 1) = ∂(1) + ∂(1). For example, in a differential field of charecteristic zero the rationals are always a subfield of the constant field.
Any field pure can be interpretted as a constant differential field.
The field Q(t) has a unique structure as a differential field, determined by setting ∂(t) = 1: the field axioms along with the axioms for derivations ensure that the derivation is differentiation with respect to t. For example, by commutativity of addition and the Leibniz law one has that ∂(u which does have a solution to this equation. A differential field with solutions to all systems of differential equations is called a differentially closed field. Such fields exist, although they do not appear as natural algebraic or geometric objects. All differential fields (of bounded cardinality) embed into a large differentially closed field. Differential fields are the objects of study in differential Galois theory.
Naturally occurring examples of derivations are partial derivatives, Lie derivatives, the Pincherle derivative, and the commutator with respect to an element of the algebra. All these examples are tightly related, with the concept of derivation as the major unifying theme.
Examples
Differential rings and differential algebras are often studied by means of the ring of pseudo-differential operators on them.
This is the ring

Multiplication on this ring is defined as
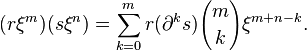
Here
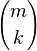 is the binomial coefficient. Note the identities
is the binomial coefficient. Note the identities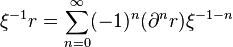
which makes use of the identity

and
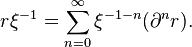

0 件のコメント:
コメントを投稿